OpenAI : Embeddings, vecteurs et géométrie niveau collège

A côté du nom fourre tout ChatGPT, il existe la notion d'Embeddings.
Vous allez voir, les embeddings sont à la portée d'un collégien qui n'a pas dormi pendant le cours de géométrie sur les vecteurs.
Comme le disait Arthur C. Clarke (certainement l'auteur le plus cité par des rédacteurs de billets de blog ;) :
Toute technologie suffisamment avancée est indiscernable de la magie.
Et la trinité AI-ML-ChatGPT s'apparente souvent à de la magie.
Pourtant, s'il est une notion fondamentale qui n'est pas de la magie, c'est bien les Embeddings.
En résumé, si on parle de texte, c'est une représentation vectorielle du texte dans un espace latent à n-dimensions (ici : 1536 dimensions).
Ouch.
Imaginons le cas concret suivant :
J'ai une liste d'articles.
Je veux connaître tous les articles qui parlent d'un sujet précis
Un vecteur, pour rappel :

Ici à 2 dimensions - 2 coordonnées. On peut imaginer 3 dimensions (l'espace), 4 dimensions (espace-temps ?),5,6 ... ou 1536. Le principe est toujours le même quel que soit le nombre de dimensions. Les vecteurs que l'on considèrera ont des coordonnées positives comprises entre 0 et 1, et sont orthonormés (leur longueur = 1), de façon à simplifier les calculs, on verra plus tard.
Ce qu'il se passe :
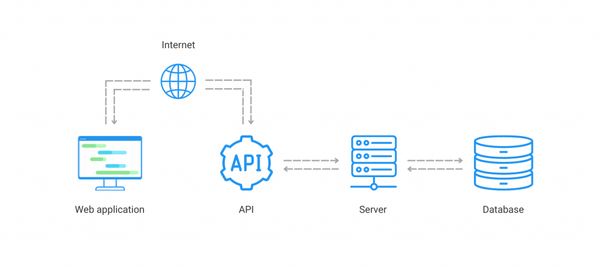
1. Ingestion : je demande à OpenAI de calculer les embeddings de chacun de mes articles
Elle est là, la magie : OpenAI, grâce à leur modèle de language et à leur colossale base d'entraînements, va calculer la représentation vectorielle de chaque article (vecteur à 1536 dimensions) et me le retourner. C'est ça l'espace latent : l'espace dans lequel ces vecteurs existent, calculés par les algos d'OpenAI.
2. Embedding de ma recherche : je demande maintenant à OpenAI de calculer l'embedding de ma recherche
Si mes articles sont des disques avec les noms des auteurs, ma recherche sera : "Trouve tous les albums des Smiths". J'ai à nouveau un vecteur à 1536 dimensions
3. Calcul de la recherche
Je n'ai plus qu'à effectuer le produit scalaire de mon vecteur de recherche sur tous les vecteurs de mes articles.
Produit scalaire ?

Produit scalaire = x’*x + y’*y
- si les 2 vecteurs sont orthogonaux : le produit scalaire = 0
- si les 2 vecteurs sont colinéaires (même direction, ici ils ont tous la même norme) : le produit scalaire = 1
Ici, on va calculer tous les produits scalaires, et on retiendra le plus grand (au maximum = 1 ici).
En effet, OpenAI, quand il calcule l'espace latent, va calculer des vecteurs "proches" quand ils ont des sens approchants, éloignés si les mots n'ont pas de rapports entre eux.
Dans la réalité, on n'obtient jamais 1, mais si le produit scalaire atteint des valeurs comme 0.8 , le résultat devient intéressant.
Un exemple :
J'ai une liste d'albums, je souhaite connaitre tous les albums des Smiths. Mince, je fais une faute d'orthographe et je tape la requête :
Find me albums from the Smoths
Les résultats :
| 0,81310874 | Album: Meat is Murder, author : the Smiths |
| 0,7876867 | Album: Hackney Diamonds, author : the Rolling Stones |
| 0,7786499 | Album: Zooropa, author : U2 |
| 0,7630683 | Album: War, author : U2 |
| 0,7842285 | Album: Mind Bomb, author : the The |
| 0,82945055 | Album: StrangeWays here we come, author : the Smiths |
On voit bien le 1er et le dernier en tête, malgré la faute, car dans l'espace latent, ces résultats sont proches.
Vous commencez à sentir la puissance de l'engin ? Qui finalement n'est pas très magique 😉?